TRANSPORTATION DATA IN A FRACTAL
DOMAIN
ABSTRACT
In following
with previous papers about international trade technology and transportation,
this paper will focus on the challenging issues posed by an overlay of surface
topology on transportation traffic in the context of the geography of nations.
But, is not only traffic and infrastructure where roads and rail exist but how these
Euclidian spaces affect cost. Here is where this paper introduces the theory of
applying fractal properties to distances and geographic forms and how mapping
of surfaces can be simplified by combining geometric properties with fractal
properties over a geographic overlay.
Introduction
One telling advantage
of fractals in this context is the property to increase the diameter of a
surface without increasing its area. This very property could be use to
describe irregular geographic surfaces of nations that can be turned into
regular polygons with known properties in Euclidian surfaces and be able to
measure variables and collect them in a linear algebra matrix in loadings of:
Direction, distance, volume, cost, and so on.
“…In
a surface of a sphere of radius R inside a cylinder, with the cylinder just
touching the equator, and cut off at the height of the top and bottom of the
sphere.
The
polygon area of the curved part of the cylinder is
2 Pi R x 2R = 4 Pi R2. This
is found by slicing the cylinder surface and rolling it out as a rectangle. It
is no accident that the cylinder surface is exactly the area of the sphere”.
Surface Analysis of Special Polygons
After
establishing the geometry between a sphere and a cylinder this paper will now introduce
a common surface--the ellipse to introduce the theory of transportation in a
fractal domain. However, this is an ellipse formed by two intersecting circles of
equal diameter where geometric distances can be defined and circle centers are
mutually shared.
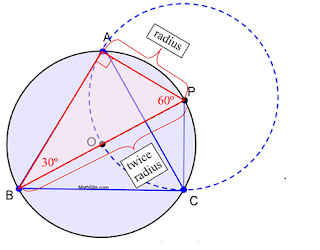
This is the junction
where the intersecting Euclidian geometry, topology and fractal geometry are
mapped and the properties of this new space are used to expand the idea of
transportation geography in a fractal domain. As an example to
this idea we’ll use the borderline of France to illustrate its topological and
fractal geometrical transformation into a Euclidian space.


This outline of the borderline is a fractal surface. It
follows that if this figure is cut and stretched into a string-line to form
a new figure in a Euclidian space we can then use plane geometry and its
properties. An ellipsis formed by two equal circles overlapping their
centers has unique properties.
Geography of France Area
643,801 km²
Coastline 3,427 km
Borders 4,176 km
Total Borderline Perimeter 7,603 km
This outline of the borderline is a fractal surface. It
follows that if this figure is cut and stretched into a string-line to form a
new figure in a Euclidian space we can then use plane geometry and its
properties. An ellipsis formed by two equal circles overlapping their centers
has unique properties.
Polygon Properties
Citations
1.- The topology of two equal spaces is homomorphic. Each
circumference of the elliptical surface =3801.5 km.
2.- A country’s area measured by length and width provides a
major and a minor axis of distance that can be described by the resulting
geometry of the intercepted circles.
3.- The effect of distance on rates is inversely proportional
to freight cost because cost is spread over a shorter or longer distance within
or between countries.
4.-Cross border rates change at the tangent line of two countries
to obtain a between countries rate. At these crossings independent matrices of
distance, commodity, handling, weight-volume and a city origin-destination can
be developed to reflect freight differentials due to infrastructure and other
factors.
5.-Each matrix of (data) n x m (measurements) has an SVD or
PCA which can be used to determine the aggregate of the most influential data
points. A cross border price is generated and related to each country’s
internal economic performance such as GDP, current account balance, GDP/ Debt
ratio, inflation rates, interest rates, budget balance and currency exchange.
Argument
for the Proposed Theory
In a generic (n x m) matrix any set of (n) items chosen with (m) measurements can be used
for decomposing the matrix and calculating the SVD based bythe following
equations:
C = UΣVᵀ followed by CᵀC = VΣᵀΣVᵀ and CV = UΣ
Where U and V are orthogonal matrices and Σ is a diagonal
matrix with corresponding eigenvalues and eigenvectors.
But to state the argument in
context we need to revisit the issue of fractal transformations. For instance: squares can be used to generate fractal polygons with
a similarity to the coast of France. Adding
a unit square to each side respectively a square with dimension one third of
the squares results from the previous iteration and both the length of the
perimeter and the total area are determined by a geometric progression. Example
for this case:
G
This area converges to 2 while the progression
for the perimeter diverges to infinity, as is the case for the Koch snowflake,
where a finite area is bounded by an infinite fractal polygon. The
resulting area fills a square with the same center as the original, but twice
the area, and rotated by π/4 radians, the perimeter touching
but never overlapping itself.
Another iteration that
can be shown with a couple lines of a programming loop in Matlab is:
=
= [1 2 3 4
5 6];
for i = 1:length(
)
disp(
(i))
end
Description
of the Polygons Referenced
1.- The circumference of
circle of radius one = 3.14 which means that a unit Vesica Piscis is formed by two
half circumferences of 1.57x 2= 3.14 or two half circles areas A=πr²/2.
2.- The Sum of the sides of a square inscribed in circle of area
3.14 = a diameter of
{\displaystyle
A_{n}={\frac {1}{5}}+{\frac {4}{5}}\sum _{k=0}^{n}\left({\frac
{5}{9}}\right)^{k}\quad {\mbox{giving}}\quad \lim _{n\rightarrow \infty }A_{n}=2\,,}=1.41 x 4= 5.65 which is a ratio of circle to square
6.32/5.65=1.12 to infinity.
3.- Euclid defined the equilateral triangle inscribed in the
Vesica Piscis using the properties of this polygon. More recent names include
the Reuleaux triangles and the Euler spherical triangles which include the
chords of a circle.
4.- Also
defined by the two circles is a triangle with sides 2 and 3 and a hypotenuse of
C²=√13.
A triangle with concurrent points is also derived.
5.- The argument made is that maximum
and minimum distances within a country can be defined with these polygons
inside and outside the Vesica Piscis.
Topological and Fractal Geometry and the Transformation
Matrix.
In this context n values used for a within
commerce matrix can be defined for each country’s boundaries, distances, economy
and financials. At the same time, m values can be used for measures of commodities
traded, volume, price and origin-destination with a daily or any other number
of n samples and m measurement for each point of the data matrix in multiple
dimensions.
What the mathematical tools of SVD and
PCA allow us to do is process large amounts of data in multidimensional space
and to reduce its dimensionality to a more manageable space in order to
discover its data pattern and correlation using the Eigen decomposition of the
covariance matrix.
Here is an exercised published by MIT
MIT Paper Singular
Value Decomposition (SVD) BE.400 / 7.548
Closing Remarks
To summarize the ideas presented herein
are based on a geographical boundary of fractal space which is then transformed
to a Euclidian space of known quantities. An unique data matrix for any country
can be used to measure international trade with as many data points and
measurements as needed which is then decomposed by its SVD of (3 matrices to obtain
a sigma diagonal matrix) which provides principal values in its diagonal responsible
for the most variation of the variance matrix entered in the initial set up
matrix. It follows that any matrix of any dimensional size can be decomposed
into its SVD components.
Needless to say the SVD is a powerful
mathematical tool to assess the prominent number of factors that have the most relevance
in commerce within a country and of trade between countries. Furthermore, the
SVD result can be used by a national government as indicator of inefficiencies
in both its financial or commercial markets and take corrective action.









